(МЕХАНИЧЕСКИЕ СИСТЕМЫ) – IV вариант
1. Основное уравнение динамики материальной точки, как известно, выражено уравнением . Дифференциальные уравнения движения произвольных точек несвободной механической системы согласно двух способов деления сил можно записать в двух формах:
(1) , где k=1, 2, 3, … , n – количество точек материальной системы.
где - масса k-той точки; - радиус вектор k-той точки, - заданная (активная) сила, действующая на k-тую точку или равнодействующая всех активных сил, действующих на k-тую точку. - равнодействующая сил реакций связей, действующая на k-тую точку; - равнодействующая внутренних сил, действующая на k-тую точку; - равнодействующая внешних сил, действующая на k-тую точку.
При помощи уравнений (1) и (2) можно стремиться решать как первую, так и вторую задачи динамики. Однако решение второй задачи динамики для системы очень усложняется не только с математической точки зрения, но и потому, что мы сталкиваемся с принципиальными трудностями. Они заключаются в том, что как для системы (1), так и для системы (2) число уравнений значительно меньше числа неизвестных.
Так, если использовать (1), то известными для второй (обратной) задачи динамики будут и , а неизвестными будут и . Векторных уравнений будет «n », а неизвестных - «2n».
Если же исходить из системы уравнений (2), то известные и часть внешних сил . Почему часть? Дело в том, что в число внешних сил входят и внешние реакции связей, которые неизвестны. К тому же неизвестными будут ещё и .
Таким образом, как система (1), так и система (2) НЕЗАМКНУТА. Нужно добавлять уравнения, учитывая уравнения связей и возможно ещё нужно накладывать некоторые ограничения на сами связи. Что делать?
Если исходить из (1), то можно пойти по пути составления уравнений Лагранжа первого рода. Но такой путь не рационален потому, что чем проще задача (меньше степеней свободы), тем труднее с точки зрения математики ее решать.
Тогда обратим внимание на систему (2), где - всегда неизвестны. Первый шаг при решении системы – это нужно исключить эти неизвестные. Следует иметь в виду, что нас, как правило, не интересуют внутренние силы при движении системы, то есть при движении системы не нужно знать, как движется каждая точка системы, а достаточно знать как движется система в целом.
Таким образом, если различными способами исключить из системы (2) неизвестные силы , то получаем некоторые соотношения, т. е. появляются некоторые общие характеристики для системы, знание которых позволяют судить о том, как движется система в общем. Эти характеристики вводятся при помощи так называемых общих теорем динамики. Таких теорем четыре:
1. Теорема о движении центра масс механической системы ;
2. Теорема об изменении количества движения механической системы ;
3. Теорема об изменении кинетического момента механической системы ;
4. Теорема об изменении кинетической энергии механической системы .
ТЕОРЕМА КОЛИЧЕСТВА ДВИЖЕНИЯ (в дифференциальной форме) .
1. Для точки: производная от количества движения точки по времени равна равнодействующей приложенных к точке сил :
или в координатной форме:
2. Для системы: производная от количества движения системы по времени равна главному вектору внешних сил системы (векторной сумме внешних сил , приложенных к системе):
или в координатной форме:
ТЕОРЕМА ИМПУЛЬСОВ (теорема количества движения в конечной форме).
1. Для точки: изменение количества движения точки за конечный промежуток времени равно сумме импульсов, приложенных к точке сил (или импульсу равнодействующей приложенных к точке сил)
или в координатной форме:
2. Для системы: изменение количества движения системы за конечный промежуток времени равно сумме импульсов внешних сил:
или в координатной форме:
Следствия: при отсутствии внешних сил количество движения системы есть величина постоянная; если внешние силы системы перпендикулярны некоторой оси, то проекция количества движения на эту ось есть величина постоянная.
ТЕОРЕМА О МОМЕНТЕ КОЛИЧЕСТВА ДВИЖЕНИЯ
1. Для точки: Производная по времени от момента количества движения точки относительно некоторого центра (оси) равна сумме моментов приложенных к точке сил относительно того же центра (оси):
2. Для системы:
Производная по времени от момента количества движения системы относительно некоторого центра (оси) равна сумме моментов внешних сил системы относительно того же центра (оси):
Следствия: если внешние силы системы не дают момента относительно данного центра (оси), то момент количества движения системы относительно этого центра (оси) есть величина постоянная.
Если силы, приложенные к точке, не дают момента относительно данного центра, то момент количества движения точки относительно этого центра есть величина постоянная и точка описывает плоскую траекторию.
ТЕОРЕМА О КИНЕТИЧЕСКОЙ ЭНЕРГИИ
1. Для точки: изменение кинетической энергии точки на конечном ее перемещении равно работе приложенных к ней активных сил (касательные составляющие реакций неидеальных связей включаются в число активных сил):
Для случая относительного движения: изменение кинетической энергии точки при относительном движении равно работе приложенных к ней активных сил и переносной силы инерции (см. "Частные случаи интегрирования") :
2. Для системы: изменение кинетической энергии системы на некотором перемещении ее точек равно работе приложенных к ней внешних активных сил и внутренних сил, приложенных к точкам системы, расстояние между которыми меняется:
Если система неизменяема (твердое тело), то ΣA i =0 и изменение кинетической энергии равно работе только внешних активных сил.
ТЕОРЕМА О ДВИЖЕНИИ ЦЕНТРА МАСС МЕХАНИЧЕСКОЙ СИСТЕМЫ . Центр масс механической системы движется как точка, масса которой равна массе всей системы M=Σm i , к которой приложены все внешние силы системы:
или в координатной форме:
где - ускорение центра масс и его проекции на оси декартовых координат; внешняя сила и ее проекции на оси декартовых координат.
ТЕОРЕМА ИМПУЛЬСОВ ДЛЯ СИСТЕМЫ, ВЫРАЖЕННАЯ ЧЕРЕЗ ДВИЖЕНИЕ ЦЕНТРА МАСС.
Изменение скорости центра масс системы за конечный промежуток времени равно импульсу внешних сил системы за тот же промежуток времени, деленному на массу всей системы.
Динамика:
Динамика материальной системы
§ 35. Теорема о движении центра масс материальной системы
Задачи с решениями
35.1 Определить главный вектор внешних сил, действующих на маховик M, вращающийся вокруг оси AB. Ось AB, укрепленная в круговой раме, в свою очередь вращается вокруг оси DE. Центр масс C маховика находится в точке пересечения осей AB и DE.
РЕШЕНИЕ
35.2 Определить главный вектор внешних сил, приложенных к линейке AB эллипсографа, изображенного на рисунке. Кривошип OC вращается с постоянной угловой скоростью ω; масса линейки AB равна M; OC=AC=BC=l.
РЕШЕНИЕ
35.3 Определить главный вектор внешних сил, действующих на колесо массы M, скатывающееся с наклонной плоскости вниз, если его центр масс C движется по закону xC=at2/2.
РЕШЕНИЕ
35.4 Колесо катится со скольжением по горизонтальной прямой под действием силы F, изображенной на рисунке. Найти закон движения центра масс C колеса, если коэффициент трения скольжения равен f, a F=5fP, где P вес колеса. В начальный момент колесо находилось в покое.
РЕШЕНИЕ
35.5 Колесо катится со скольжением по горизонтальной прямой под действием приложенного к нему вращающего момента. Найти закон движения центра масс C колеса, если коэффициент трения скольжения равен f. В начальный момент колесо находилось в покое.
РЕШЕНИЕ
35.6 Вагон трамвая совершает вертикальные гармонические колебания на рессорах амплитуды 2,5 см и периода T=0,5 c. Масса кузова с нагрузкой 10 т, масса тележки и колес 1 т. Определить силу давления вагона на рельсы.
РЕШЕНИЕ
35.7 Определить силу давления на грунт насоса для откачки воды при его работе вхолостую, если масса неподвижных частей корпуса D и фундамента E равна M1, масса кривошипа OA=a равна M2, масса кулисы B и поршня C равна M3. Кривошип OA, вращающийся равномерно с угловой скоростью ω, считать однородным стержнем.
РЕШЕНИЕ
35.8 Использовав данные предыдущей задачи, считать, что насос установлен на упругом основании, коэффициент упругости которого равен c. Найти закон движения оси O кривошипа OA по вертикали, если в начальный момент ось O находилась в положении статического равновесия и ей была сообщена по вертикали вниз скорость v0. Взять начало отсчета оси x, направленной вертикально вниз, в положении статического равновесия оси O. Силами сопротивления пренебречь.
РЕШЕНИЕ
35.9 Ножницы для резки металла состоят из кривошипно-ползунного механизма OAB, к ползуну B которого прикреплен подвижный нож. Неподвижный нож укреплен на фундаменте C. Определить давление фундамента на грунт, если длина кривошипа r, масса кривошипа M1, длина шатуна l, масса ползуна B с подвижным ножом M2, масса фундамента C и корпуса D равна M3. Массой шатуна пренебречь. Кривошип OA, равномерно вращающийся с угловой скоростью ω, считать однородным стержнем.
РЕШЕНИЕ
35.10 Электрический мотор массы M1 установлен без креплений на гладком горизонтальном фундаменте; на валу мотора под прямым углом закреплен одним концом однородный стержень длины 2l и массы M2, на другой конец стержня насажен точечный груз массы M3; угловая скорость вала равна ω. Определить: 1) горизонтальное движение мотора; 2) наибольшее горизонтальное усилие R, действующее на болты, если ими будет закреплен кожух электромотора на фундаменте.
РЕШЕНИЕ
35.11 По условиям предыдущей задачи вычислить ту угловую скорость ω вала электромотора, при которой электромотор будет подпрыгивать над фундаментом, не будучи к нему прикреплен болтами.
РЕШЕНИЕ
35.12 При сборке электромотора его ротор B был эксцентрично насажен на ось вращения C1 на расстоянии C1C2=a, где C1 центр масс статора A, а C2 центр масс ротора B. Ротор равномерно вращается с угловой скоростью ω. Электромотор установлен посередине упругой балки, статический прогиб которой равен Δ; M1 масса статора, M2 масса ротора. Найти уравнение движения точки C1 по вертикали, если в начальный момент она находилась в покое в положении статического равновесия. Силами сопротивления пренебречь. Начало отсчета оси x взять в положении статического равновесия точки C1.
РЕШЕНИЕ
35.13 Электрический мотор массы M1 установлен на балке, жесткость которой равна c. На вал мотора насажен груз массы M2 на расстоянии l от оси вала. Угловая скорость мотора ω=const. Определить амплитуду вынужденных колебаний мотора и критическое число его оборотов в минуту, пренебрегая массой балки и сопротивлением движению.
РЕШЕНИЕ
35.14 На рисунке изображена крановая тележка A массы M1, которая заторможена посередине балки BD. В центре масс C1 тележки подвешен трос длины l с привязанным к нему грузом C2 массы M2. Трос с грузом совершает гармонические колебания в вертикальной плоскости. Определить: 1) суммарную вертикальную реакцию балки BD, считая ее жесткой; 2) закон движения точки C1 в вертикальном направлении, считая балку упругой с коэффициентом упругости, равным c. В начальный момент балка, будучи недеформированной, находилась в покое в горизонтальном положении. Считая колебания троса малыми, принять: sin φ≈φ, cos φ≈1. Начало отсчета оси y взять в положении статического равновесия точки C1. Массой троса и размерами тележки по сравнению с длиной балки пренебречь.
РЕШЕНИЕ
35.15 Сохранив данные предыдущей задачи и считая балку BD жесткой, определить: 1) суммарную горизонтальную реакцию рельсов; 2) в предположении, что тележка не заторможена, закон движения центра масс C1 тележки A вдоль оси x. В начальный момент точка C1 находилась в покое в начале отсчета оси x. Трос совершает колебания по закону φ=φ0 cos ωt.
РЕШЕНИЕ
35.16 На средней скамейке лодки, находившейся в покое, сидели два человека. Один из них, массы M1=50 кг, переместился вправо на нос лодки. В каком направлении и на какое расстояние должен переместиться второй человек массы M2=70 кг для того, чтобы лодка осталась в покое? Длина лодки 4 м. Сопротивлением воды движению лодки пренебречь.
РЕШЕНИЕ
35.17 На однородную призму A, лежащую на горизонтальной плоскости, положена однородная призма B; поперечные сечения призм прямоугольные треугольники, масса призмы A втрое больше массы призмы B. Предполагая, что призмы и горизонтальная плоскость идеально гладкие, определить длину l, на которую передвинется призма A, когда призма B, спускаясь по A, дойдет до горизонтальной плоскости.
РЕШЕНИЕ
35.18 По горизонтальной товарной платформе длины 6 м и массы 2700 кг, находившейся в начальный момент в покое, двое рабочих перекатывают тяжелую отливку из левого конца платформы в правый. В какую сторону и насколько переместится при этом платформа, если общая масса груза и рабочих равна 1800 кг? Силами сопротивления движению платформы пренебречь.
РЕШЕНИЕ
35.19 Два груза M1 и M2, соответственно массы M1 и M2, соединенные нерастяжимой нитью, переброшенной через блок A, скользят по гладким боковым сторонам прямоугольного клина, опирающегося основанием BC на гладкую горизонтальную плоскость. Найти перемещение клина по горизонтальной плоскости при опускании груза M1 на высоту h=10 см. Масса клина M=4M1=16M2; массой нити и блока пренебречь.
РЕШЕНИЕ
35.20 Три груза массы M1=20 кг, M2=15 кг и M3=10 кг соединены нерастяжимой нитью, переброшенной через неподвижные блоки L и N. При опускании груза M1 вниз груз M2 перемещается по верхнему основанию четырехугольной усеченной пирамиды ABCD массы M=100 кг вправо, а груз M3 поднимается по боковой грани AB вверх. Пренебрегая трением между усеченной пирамидой ABCD и полом, определить перемещение усеченной пирамиды ABCD относительно пола, если груз M1 опустится вниз на 1 м. Массой нити пренебречь.
РЕШЕНИЕ
35.21 Подвижной поворотный кран для ремонта уличной электросети установлен на автомашине массы 1 т. Люлька K крана, укрепленная на стержне L, может поворачиваться вокруг горизонтальной оси O, перпендикулярной плоскости рисунка. В начальный момент кран, занимавший горизонтальное положение, и автомашина находились в покое. Определить перемещение незаторможенной автомашины, если кран повернулся на 60°. Масса однородного стержня L длины 3 м равна 100 кг, а люльки K 200 кг. Центр масс C люльки K отстоит от оси O на расстоянии OC=3,5 м. Сопротивлением движению пренебречь.
Министерство образования и науки Российской Федерации
Федеральное государственное бюджетное образовательное учреждение высшего профессионального образования
«Кубанский государственный технологический университет»
Теоретическая механика
Часть 2 динамика
Утверждено Редакционно-издательским
советом университета в качестве
учебного пособия
Краснодар
УДК 531.1/3 (075)
Теоретическая механика. Часть 2. Динамика: Учебное пособие / Л.И.Драйко; Кубан. гос. технол.ун-т. Краснодар, 2011. 123 с.
ISBN 5-230-06865-5
Излагается в краткой форме теоретический материал, даны примеры решения задач, большинство из которых отражает реальные вопросы техники, уделено внимание выбору рационального способа решения.
Предназначено для бакалавров заочной и дистанционной форм обучения строительных, транспортных и машиностроительных направлений.
Табл. 1 Илл. 68 Библиогр. 20 назв.
Научный редактор канд.техн.наук,доц. В.Ф.Мельников
Рецензенты: зав.кафедрой теоретической механики и теории механизмов и машин Кубанского аграрного университета проф. Ф.М. Канарев; доцент кафедры теоретической механики Кубанского государственного технологического университета М.Е. Мултых
Печатается по решению Редакционно-издательского совета Кубанского государственного технологического университета.
Переиздание
ISBN 5-230-06865-5 КубГТУ 1998г.
Предисловие
Данное учебное пособие предназначено для студентов заочной формы обучения строительных, транспортных и машиностроительных специальностей, но может быть использовано при изучении раздела «Динамика» курса теоретической механики студентами заочниками других специальностей, а также студентами дневной формы обучения при самостоятельной работе.
Пособие составлено в соответствии с действующей программой курса теоретической механики, охватывает все вопросы основной части курса. Каждый раздел содержит краткий теоретический материал, снабженный иллюстрациями и методическими рекомендациями для его использования при решении задач. В пособии разобрано решение 30 задач, отражающих реальные вопросы техники и соответствующих контрольным заданиям для самостоятельного решения. Для каждой задачи представлена расчетная схема, наглядно иллюстрирующая решение. Оформление решения соответствует требованиям, предъявляемым к оформлению контрольных работ студентов-заочников.
Автор выражает глубокую признательность преподавателям кафедры теоретической механики и теории механизмов и машин Кубанского аграрного университета за большой труд по рецензированию учебного пособия, а также преподавателям кафедры теоретической механики Кубанского государственного технологического университета за ценные замечания и советы по подготовке учебного пособия к изданию.
Все критические замечания и пожелания будут приняты автором с благодарностью и в дальнейшем.
Введение
Динамика является наиболее важным разделом теоретической механики. Большинство конкретных задач, которые приходится в инженерной практике, относится к динамике. Используя выводы статики и кинематики, динамика устанавливает общие законы движения материальных тел под действием приложенных сил.
Простейшим материальным объектом является материальная точка. За материальную точку можно принять материальное тело любой формы, размерами которого в рассматриваемой задаче можно пренебречь. За материальную точку можно принимать тело конечных размеров, если различие в движении его точек для данной задачи не существенно. Это бывает в случае, когда размеры тела малы по сравнению с расстояниями, которые проходят точки тела. Каждую частицу твердого тела можно считать материальной точкой.
Силы, приложенные к точке или материальному телу, в динамике оцениваются по их динамическому воздействию, т. е. по тому, как они изменяют характеристики движения материальных объектов.
Движение материальных объектов с течением времени совершается в пространстве относительно определенной системы отсчета. В классической механике, опирающейся на аксиомы Ньютона, пространство считается трехмерным, его свойства не зависят от движущихся в нем материальных объектов. Положение точки в таком пространстве определяется тремя координатами. Время не связано с пространством и движением материальных объектов. Оно считается одинаковым для всех систем отсчета.
Законы динамики описывают движение материальных объектов по отношению к абсолютным осям координат, условно принятым за неподвижные. Начало абсолютной системы координат принимается в центре Солнца, а оси направляются на отдаленные, условно не подвижные звезды. При решении многих технических задач условно не подвижными можно считать координатные оси, связанные с Землей.
Параметры механического движения материальных объектов в динамике устанавливаются путем математических выводов из основных законов классической механики.
Первый закон (закон инерции):
Материальная точка сохраняет состояние покоя или равномерного и прямолинейного движения до тех пор, пока действие каких-либо сил не выведет ее из этого состояния.
Равномерное и прямолинейное движение точки называют движением по инерции. Покой является частным случаем движения по инерции, когда скорость точки равна нулю.
Всякая материальная точка обладает инертностью, т. е. стремится сохранить состояние покоя или равномерного прямолинейного движения. Система отсчета, по отношению к которой выполняется закон инерции, называется инерциальной, а движение, наблюдаемое по отношению к этой системе, называется абсолютным. Любая система отсчета, совершающая относительно инерциальной системы поступательное прямолинейное и равномерное движение, будет также инерциальной системой.
Второй закон (основной закон динамики):
Ускорение
материальной точки относительно
инерциальной системы отсчета
пропорционально приложенной к точке
силе и совпадает с силой по направлению:
 .
.
Из основного закона
динамики следует, что при силе
 ускорение
ускорение .
Масса точки характеризует степень
сопротивляемости точки изменению ее
скорости, т. е. является мерой инертности
материальной точки.
.
Масса точки характеризует степень
сопротивляемости точки изменению ее
скорости, т. е. является мерой инертности
материальной точки.
Третий закон (закон действия и противодействия):
Силы, с которыми два тела действуют друг на друга, равны по модулю и направлены вдоль одной прямой в противоположные стороны.
Силы, именуемые действием и противодействием, приложены к разным телам и поэтому уравновешенной системы не образуют.
Четвертый закон (закон независимости действия сил):
При одновременном действии нескольких сил ускорение материальной точки равно геометрической сумме ускорений, которые имела бы точка при действии каждой силы в отдельности:
 , где
, где
 ,
, ,…,
,…, .
.

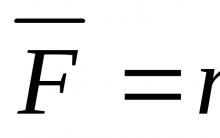






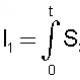


Пышки на кефире жареные
Персидский язык (фарси) Какие языки относятся к фарси
График sin 0. Урок математики. Тема: "Функция y=sin x, ее свойства и график". Выражение синуса через косинус
Понятие и виды углов Фигуры при пересечении прямых
К чему снится спасать человека Сонник толкование снов к чему снится спасение